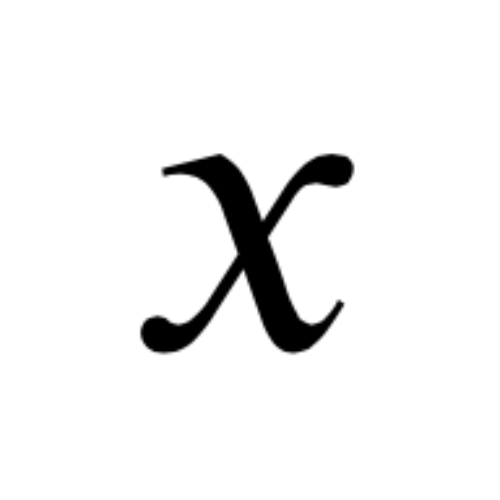Algebra is a branch of mathematics that uses symbols and letters to represent numbers and quantities in formulas and equations. It provides a systematic way to express mathematical relationships and solve problems.

Basic Concepts

• Variables: Symbols (such as x and y) that represent unknown values.
• Constants: Fixed values, such as 3, -5, or 10.
• Expressions: A combination of numbers, variables, and operations (e.g., \(3x + 5\)).
• Equations: A statement that two expressions are equal (e.g., \(2x + 3 = 7\)).

Basic Operations in Algebra

Algebra follows the same basic arithmetic operations:

• Addition: \( a + b \)
• Subtraction: \( a - b \)
• Multiplication: \( a \times b \) or \( ab \)
• Division: \( \frac{a}{b} \) or \( a \div b \)

Properties of Algebra

Algebra follows several fundamental properties:

• Commutative Property: \( a + b = b + a \) and \( ab = ba \)
• Associative Property: \( (a + b) + c = a + (b + c) \)
• Distributive Property: \( a(b + c) = ab + ac \)

Solving Equations

To solve an equation, we aim to find the value of the unknown variable. Here’s an example:

Example: Solve for \( x \) in the equation \( 2x + 3 = 7 \).

Step 1: Subtract 3 from both sides

\[ 2x = 7 - 3 \]

Step 2: Divide both sides by 2

\[ x = \frac{4}{2} = 2 \]

Linear Equations

A linear equation is an equation of the form:

\[ ax + b = 0 \]

where \( a \) and \( b \) are constants. The solution is:

\[ x = -\frac{b}{a} \]

Quadratic Equations

A quadratic equation has the form:

\[ ax^2 + bx + c = 0 \]

The solutions are given by the quadratic formula:

\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]

Exponents and Powers

Exponents represent repeated multiplication. The basic rules include:

• Product Rule: \( a^m \times a^n = a^{m+n} \)
• Quotient Rule: \( \frac{a^m}{a^n} = a^{m-n} \)
• Power Rule: \( (a^m)^n = a^{mn} \)

Applications of Algebra

Algebra is used in various fields such as physics, engineering, computer science, and economics. Some common applications include:

• Solving for unknowns in physics equations.
• Calculating profit and loss in business.
• Developing algorithms in programming.

Conclusion

Understanding the fundamentals of algebra is essential for solving mathematical problems and real-world applications. By mastering the basic concepts, operations, and properties, you can build a strong foundation for advanced mathematics.