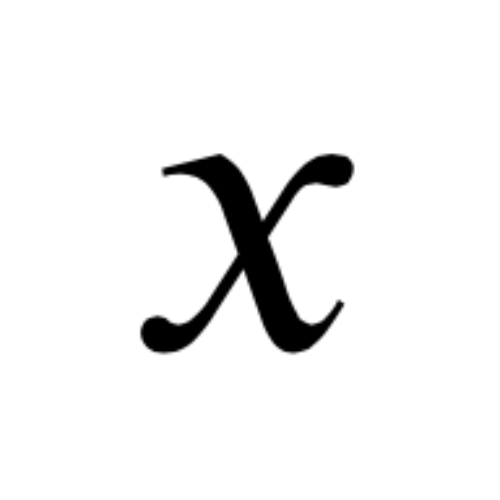Introduction to Variables, Constants, and Algebraic Expressions

In algebra, we use symbols to represent numbers and relationships. These symbols help us write equations and solve problems more efficiently. The three key components we will explore are variables, constants, and algebraic expressions.

Variables

A variable is a symbol, usually a letter, that represents an unknown or changing number. For example, in the equation:

\[ x + 5 = 12 \]

the letter x is a variable because its value is unknown until we solve the equation.

Constants

A constant is a fixed number that does not change. In the expression:

\[ 3x + 7 \]

the number 7 is a constant because its value remains the same regardless of what x is.

Algebraic Expressions

An algebraic expression is a combination of variables, constants, and mathematical operations (addition, subtraction, multiplication, and division). Unlike an equation, an expression does not have an equal sign.

Examples of algebraic expressions include:

• \( 2x + 3 \) (a linear expression)
• \( 5y^2 - 4y + 6 \) (a quadratic expression)
• \( \frac{3}{x} + 2 \) (a rational expression)

Evaluating Algebraic Expressions

To evaluate an algebraic expression, we substitute a given value for the variable and simplify. For example, if \( x = 4 \), then:

\[ 2x + 3 = 2(4) + 3 = 8 + 3 = 11 \]

Conclusion

Understanding variables, constants, and algebraic expressions is essential for solving equations and working with more advanced math concepts. Mastering these basics will help you build a strong foundation in algebra.