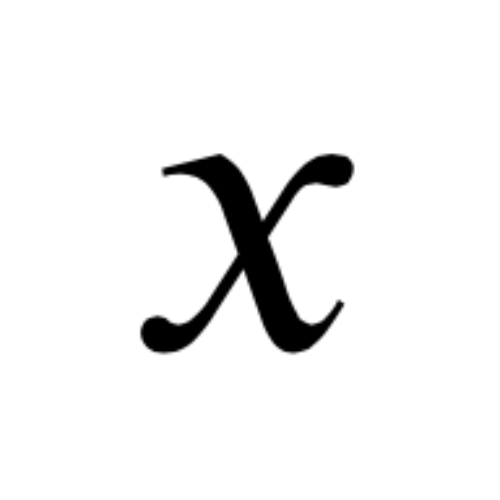When solving mathematical expressions, it is important to follow the correct sequence of operations. The order of operations ensures that everyone evaluates expressions the same way and gets the correct result.

PEMDAS Rule

PEMDAS is an acronym that helps us remember the order of operations:

• P – Parentheses: Solve expressions inside parentheses \( () \) or brackets \( [] \) first.
• E – Exponents: Calculate powers and roots.
• M and D – Multiplication and Division: Perform these operations from left to right.
• A and S – Addition and Subtraction: Perform these operations from left to right.

Example of Order of Operations

Let's evaluate the expression:

\[ 3 + 6 \times (5 - 2)^2 \div 3 \]

Following PEMDAS:

1. Parentheses: \( 5 - 2 = 3 \)
2. Exponents: \( 3^2 = 9 \)
3. Multiplication and Division: \( 6 \times 9 = 54 \), then \( 54 \div 3 = 18 \)
4. Addition: \( 3 + 18 = 21 \)

So, \( 3 + 6 \times (5 - 2)^2 \div 3 = 21 \).

Common Mistakes

Ignoring the order of operations can lead to incorrect results. For example:

\[ 3 + 6 \times 5 - 2 \]

If we add first: \( 3 + 6 = 9 \), then multiply: \( 9 \times 5 = 45 \), and subtract: \( 45 - 2 = 43 \), we get the wrong answer.

The correct approach follows PEMDAS:

• Multiplication first: \( 6 \times 5 = 30 \)
• Addition and Subtraction: \( 3 + 30 - 2 = 31 \)

So, the correct answer is \( 31 \), not \( 43 \).

Conclusion

Following the order of operations using PEMDAS ensures that mathematical expressions are evaluated correctly. Practicing this rule will help you avoid mistakes and improve your problem-solving skills in algebra.