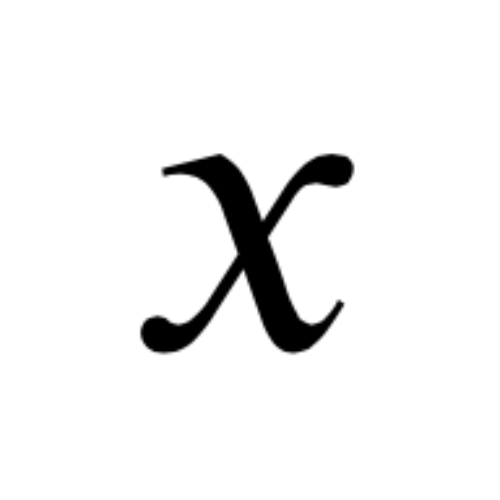In algebra, simplifying expressions makes them easier to work with by reducing complexity while keeping the value unchanged. Two key techniques for simplification are combining like terms and using the distributive property.

Combining Like Terms

Like terms are terms that have the same variable raised to the same power. Only like terms can be combined by adding or subtracting their coefficients.

For example, in the expression:

\[ 3x + 5x - 2 + 4 \]

the terms \( 3x \) and \( 5x \) are like terms, and \( -2 \) and \( 4 \) are constants that can be combined:

\[ (3x + 5x) + (-2 + 4) = 8x + 2 \]

Using the Distributive Property

The distributive property allows us to multiply a term outside parentheses by each term inside the parentheses:

\[ a(b + c) = ab + ac \]

For example:

\[ 4(2x + 3) \]

Using the distributive property:

\[ 4 \times 2x + 4 \times 3 = 8x + 12 \]

Example of Simplifying an Expression

Let's simplify:

\[ 2(x + 3) + 4x - 5 \]

First, apply the distributive property:

\[ 2x + 6 + 4x - 5 \]

Now, combine like terms:

\[ (2x + 4x) + (6 - 5) = 6x + 1 \]

Conclusion

Simplifying algebraic expressions makes equations easier to work with. By combining like terms and using the distributive property, we can rewrite expressions in a more manageable form, helping us solve problems efficiently.