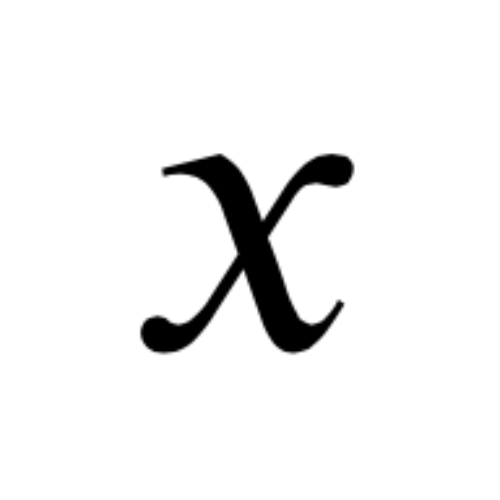Solving basic linear equations involves isolating the variable to determine its value. These equations can be categorized as one-step or two-step equations.

One-Step Equations

One-step equations require a single operation to isolate the variable. The goal is to undo the operation using inverse operations.

For example:

\[ x + 5 = 12 \]

To solve for \( x \), subtract 5 from both sides:

\[ x = 12 - 5 \]

\[ x = 7 \]

Another example:

\[ 4x = 20 \]

To isolate \( x \), divide both sides by 4:

\[ x = \frac{20}{4} \]

\[ x = 5 \]

Two-Step Equations

Two-step equations require two inverse operations to isolate the variable.

For example:

\[ 3x + 4 = 19 \]

Step 1: Subtract 4 from both sides:

\[ 3x = 15 \]

Step 2: Divide by 3:

\[ x = \frac{15}{3} \]

\[ x = 5 \]

Checking Your Solution

To verify your solution, substitute the value of \( x \) back into the original equation and check if both sides are equal.

For \( 3x + 4 = 19 \), substituting \( x = 5 \):

\[ 3(5) + 4 = 15 + 4 = 19 \]

Since both sides are equal, the solution is correct.

Conclusion

Solving one-step and two-step equations involves using inverse operations to isolate the variable. Mastering these techniques is essential for solving more complex algebraic equations.