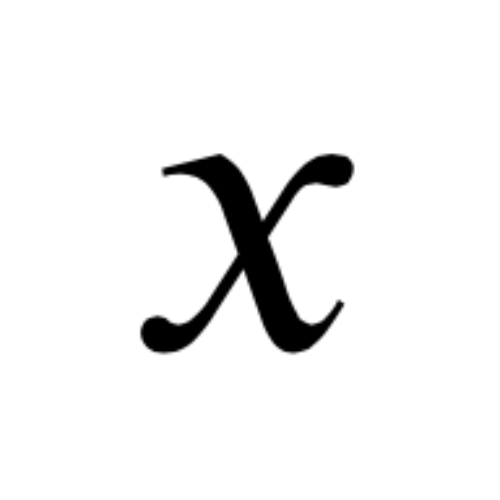Solving multi-step equations requires performing multiple operations to isolate the variable. These equations may also include variables on both sides, which need to be combined before solving.

Solving Multi-Step Equations

To solve multi-step equations, follow these steps:

1. Simplify each side (distribute and combine like terms).
2. Move variables to one side.
3. Isolate the variable using inverse operations.

Example:

\[ 2(x + 3) - 4 = 10 \]

Step 1: Distribute:

\[ 2x + 6 - 4 = 10 \]

Step 2: Simplify constants:

\[ 2x + 2 = 10 \]

Step 3: Subtract 2 from both sides:

\[ 2x = 8 \]

Step 4: Divide by 2:

\[ x = 4 \]

Solving Equations with Variables on Both Sides

When variables appear on both sides, move all variable terms to one side and constants to the other.

Example:

\[ 3x + 5 = 2x + 11 \]

Step 1: Subtract \( 2x \) from both sides:

\[ x + 5 = 11 \]

Step 2: Subtract 5 from both sides:

\[ x = 6 \]

Checking Your Solution

Always substitute the solution back into the original equation to verify:

For \( 3x + 5 = 2x + 11 \), substituting \( x = 6 \):

\[ 3(6) + 5 = 2(6) + 11 \]

\[ 18 + 5 = 12 + 11 \]

\[ 23 = 23 \]

Since both sides are equal, the solution is correct.

Conclusion

Solving multi-step equations and equations with variables on both sides requires careful application of inverse operations. Practicing these steps helps build confidence in solving more complex algebraic equations.