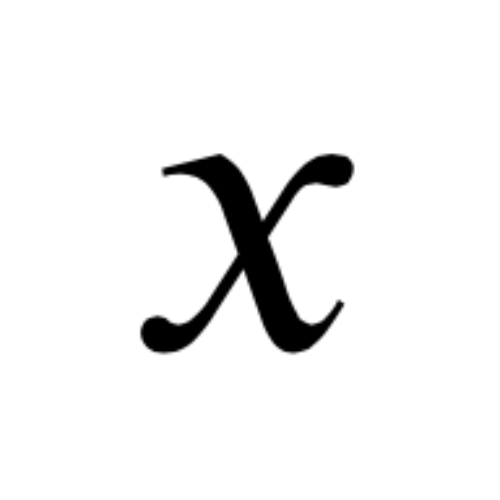Absolute value represents the distance of a number from zero on the number line, always resulting in a non-negative value. Solving absolute value equations involves considering both positive and negative solutions.

Understanding Absolute Value Equations

An absolute value equation has the form:

\[ |x| = a \]

This means that \( x \) can be either \( a \) or \( -a \), since absolute value measures distance.

Example:

\[ |x - 3| = 5 \]

To solve, set up two equations:

\[ x - 3 = 5 \] or \[ x - 3 = -5 \]

Solving both:

\[ x = 8 \] or \[ x = -2 \]

Solving More Complex Absolute Value Equations

For equations involving additional operations, isolate the absolute value expression first.

Example:

\[ 2 |x + 4| - 6 = 8 \]

Step 1: Add 6 to both sides:

\[ 2 |x + 4| = 14 \]

Step 2: Divide by 2:

\[ |x + 4| = 7 \]

Step 3: Remove absolute value by setting up two equations:

\[ x + 4 = 7 \] or \[ x + 4 = -7 \]

Step 4: Solve for \( x \):

\[ x = 3 \] or \[ x = -11 \]

Checking for Extraneous Solutions

Sometimes, solving absolute value equations can produce extraneous (false) solutions. Always substitute solutions back into the original equation to verify their validity.

Conclusion

Solving absolute value equations requires considering both positive and negative cases. By isolating the absolute value expression and solving the resulting equations, we can find all possible solutions.